データを読む力を高める＝集計／分析編【第3回】

　前回でデータについて理解ができたと思います。それでは、データを読む力の根幹をなす「集計」と「分布」についての理解を深めていきましょう。

　集計も分布も学生時代に習ったはずですが、その経験がデータに対する好き嫌いを生んでいるかもしれません。しかし、その後に、みなさんが経験されたことと考え合わせれば、理解度・納得度は大きく違うはずです。以下では、いくつか事例を挙げますが、ご自身の身近な例に置き換えながら読み進めてください。

集計：情報を収集し集約した形で表現する

　さて集計ですが、集計とは、レポートや分析を目的に、そこで使用する情報を収集し、それを集約した形式で表現することです。その結果として私たちが目にしているのが、各種のグラフや、アナリストレポート、販売実績などです。

　集計で得られる項目には、「最小値（Min）」「最大値（Max）」「合計（Sum）」「カウント（Count）」」「平均（Average）」「中央値（Median）」「最頻値（Mode）」があります。

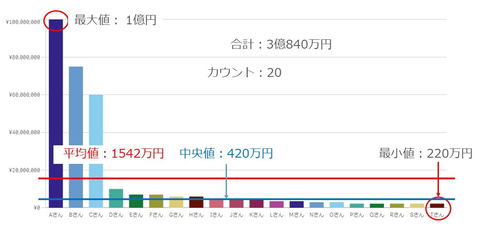
　それぞれを具体的に説明するために、ここでは社員を募集中のABCコーポレーションというスタートアップ企業の会社案内を考えてみましょう。図1は、ABCコーポレーションの社員全員の年収を示した棒グラフです。

図1：ABCコーポレーションの社員全員の年収

　簡単な項目からいえば、最小値と最大値は、その名の通り、最も小さな値と最も大きな値です。両者により、値が存在する範囲がわかります。

　合計値は、観察値を足し合わせたものです。ABCコーポレーションの例では、全社員に払った給与の合算であり、人件費を考える時に有効です。カウントは観測対象の数で、この例では社員の数です。

　さて人材募集に向けた会社紹介において給与に関しては、どのように集計した結果を示すのが適切でしょうか。

　まずは平均です。平均は合計をカウントで割るだけなので簡単です。ABCコーポレーションの平均給与を計算すると1542万円になります。しかし実際は、3人だけが著しく高い給与で、それ以外と大きく差が開いています。

　これでは、平均給与を見て「いい待遇だ」と期待した応募者を落胆させかねません。この例では平均には歪みがあるため、平均を示すことは適切ではないかもしれません。

　では中央値はどうでしょうか。中央値は値の大きさ順に並べた時に中央にある値です。たとえばカウントが5で値が「1、2、4、5、28」なら、中央は3番目なので中央値は「4」になります。カウントが偶数の場合は、中央にある2つの値で平均をとります。

　ABCコーポレーションの中央値は420万円です。これなら社員が得る給与額としてのイメージとしてはより適切そうです。この例では、平均と中央値を比べると1100万円ほどの差があり、集計方法の選択を間違えると、これほど大きな差が生まれてしまうのです。

　平均と中央値の、どちらを選ぶかはデータの分布状況によります。詳細は後述しますが、正規分布、言い換えると左右で対称的なら平均がいいでしょう。逆に正規分布ではない、つまり左右で対称的ではない、あるいは他とは大きく異なる値（外れ値）があるときなどには中央値を採用する方がより適切な場合があります。

　最後に、最頻値は最も頻繁に登場する値です。ABCコーポレーションでは、新人の給与である220万円が最頻値です。最頻値は他に比較してあまり頻繁に使われることはありませんが、該当者が最も多い値や階級を示すため、多数派の実態を把握するために用いられることがあります。