- Column
- 学校では学べないデジタル時代のデータ分析法
ビッグデータの分析は客観的から主観的へ、ベイズ推定が注目される理由【第3回】
前回、経営層を含めたビジネスリーダーが知りたいのは、最適な答えであり、それを見いだすための相関関係/因果関係であると指摘した。分析自体は手段である。だが、分析の方法を正しく理解していなければ、手段としても正しくは使えない。今回は、分析方法、なかでも、ビッグデータ分析で「ベイズ推定」が注目される理由を説明する。
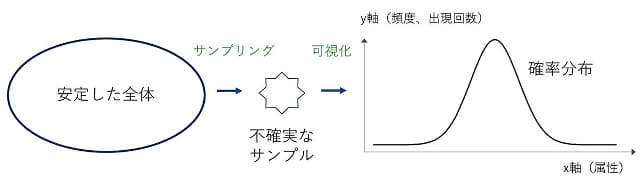
従来の統計学では、分析対象の“全体”が比較的安定していた(図1)。データ量の伸びが、想定内の線型的な伸びでしかなかったからだ。日本の人口といった安定した全体から取り出したサンプル(標本)は、全体を代表し、ごく単純な“事実”を示す。事実は、グラフにより表現されることが多い。統計は、グラフにより“結果”が見えており、そこから“原因”を考えていく「逆問題」である。
分析対象が“不安定”になり客観的な分析が限界に
サンプリングの方法やサンプル数にもよるが、一般にサンプルは不安定なものである。しかし、サンプル数が多ければ多いほど「高度に有意」、すなわち、そのデータには信頼性があると判定する。そこでは、少数のデータをサンプリングすることに意味はない。
属性を x 軸に、数量(頻度とも表現できる)をy 軸にとると、世の中のさまざまな現象が分布として現れる。これを「確率分布」と言う。確率分布とは、データを属性で見る場合、その属性の起こりやすさ、言い換えれば、頻度を記述するものである。x 軸にデータの属性が持つ特徴が左側から「低・中・高」と並び、y 軸にデータの数量が示される。
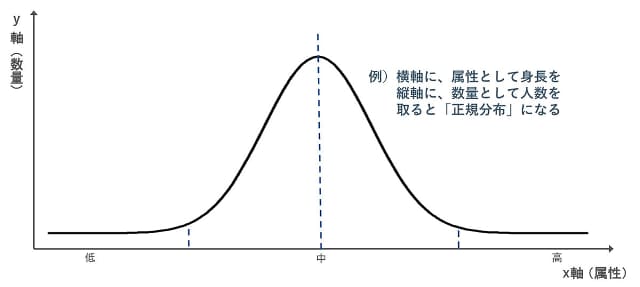
確率分布の代表が、「正規分布」「対数正規分布」「べき分布」などだ。それぞれの詳細は次回に説明するが、日本人の身長や、全国模試の点数などは正規分布に分類される(図2)。所得分布は対数正規分布に、さまざまな自然現象や株価、為替レートなどビジネスに関わる現象は、べき分布に分類される。
確率分布は、データのみに基づき、あくまでも客観的なものである。筆者が講演やプレゼンテーションなどでホワイトボードを使って説明する際は、必ずと言っていいほど正規分布を使う。18~19世紀に、自然現象における偶然性を支配する唯一のモデルとして正当化された。自然界における、あらゆるものの寸法や、製品の仕様など、多数の独立した現象が正規分布に当てはまる。グラフの形は、中央が最も高く左右対称な「釣り鐘型」である。