「可視化」でビギナーズラックもAmazonの戦略も理由が見えてくる【第4回】

　データ分析の手法には「可視化」「分類」「予測」の3つがある。確率分布などによって「可視化」し、クラスター分析や主成分分析などにより「分類」する。判別分析やロジスティック回帰分析などで「予測」が可能になる。こうしたデータ分析により、熟練者の経験と勘に頼らない状況判断や機械の故障予知などができれば、意思決定速度の向上や新たなビジネスモデル構築が可能になると期待されている。

ビギナーズラックを説明できる「正規分布」

　まず、可視化について説明する。可視化で、誰もがすぐに思い付くのがグラフである。棒グラフ、円グラフ、折れ線グラフなどが代表的だ。

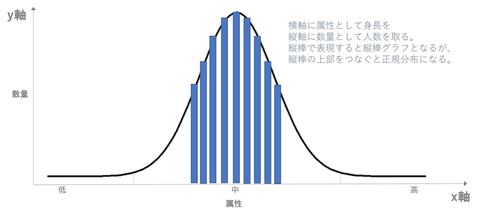
　縦棒グラフについて考えてみる（図1）。横軸（x軸）がデータの属性を表現し、縦軸（y軸）がデータの出現回数である。たとえば、日本人の中学3年生の身長をグラフで表現しようとすれば、x軸が身長で、y軸が人数である。縦棒の上端を結んでいけば、誰もが知っている「正規分布」が現れる。

図1：身長を表現した棒グラフと正規分布の関係

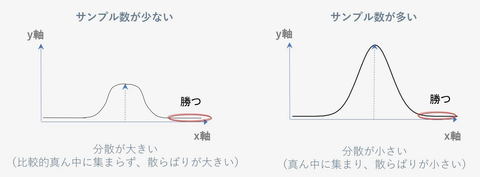
　賭け事などでは「ビギナーズラック」が起こる。その理由は、正規分布を見れば理解できるだろう。図1のグラフで、x軸を賭け事で勝った金額にすると、右側に行くほど大勝ちすることになる。サンプル数が多くても少なくても、x軸の右側の領域はさほど変わらない。つまり、回数を少なくしたほうが確率的には勝てるということだ（図2）。回数を増やせば増やすほど、平均値の真ん中の領域が増えていくからである。これを『大数の法則』という。

図2：ビギナーズラックが起こる理由は正規分布で理解できる

社会現象の歪さを表す「対数正規分布」

　ビギナーズラックなどの正規分布は“足し算”で現れる分布である。これに対し、“掛け算”で現れるのが「対数正規分布」だ。対数とは、10、100（ = 10の2乗）、1000（ = 10の3乗）、10000（ = 10の4乗）、･･･と指数的に増えていく数において、その桁数（10の例では、2、3、4、･･･）を表したものだ。

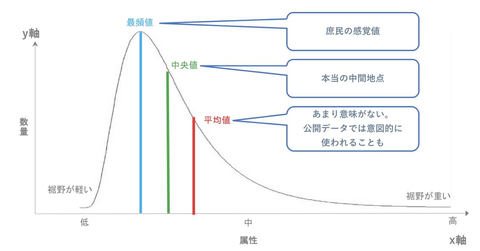
　日本人の所得をグラフにすると、左右対称ではなく、右端がゆっくりと0へと収束していく（図3）。これを「裾野が重い」と言う。逆に、左端のように急激に0へと収束する状態を「裾野が軽い」と表現する。

図3：対数正規分布では「平均値」に騙されやすい

　このグラフで騙されやすいのが「平均値」だ。平均値だけをみると庶民の実感とはズレがでてくる。注目すべきは、平均値ではなく、「中央値（ x軸で最下位とトップの真ん中の値）」や「最頻値（ x軸で一番頻度が多い値）」だ。なお、このグラフの数字の対数（log）を取ると正規分布が現れるので、これを「対数正規分布」という。

　筆者の推測ではあるが、所得の場合、経営層など給与が高い人が社員の給与額を決めるため、人工的な要素が加わり、グラフは左右対称ではなくなるのだろう。実際、企業の役員報酬は、利益連動とストックオプションが中心であり、利益を増やし株価を上げることが至上命題だ。従業員の給与を上げようとは考えない。

　自然現象は滑らかなグラフに、人工的な現象は歪なグラフになる。ほかにも、体重の分布などが対数正規分布になる。身長と違って体重は、人工的な要因（やせたい願望など）が強い影響を与えるからかもしれない。