- Column
- 学校では学べないデジタル時代のデータ分析法
正しい分析に向けデータの特性と関係性のパターンを知る【第8回】
新しい分析には新しいデータ「オープンデータ」を活用する
いずれにせよ、Any Dataの分析では未知の情報を見いだすことに価値がある。これまでにない新しいことに挑むには、新しいデータも分析しなければならない。筆者が新しいデータとして用いているのが「Open Data(自由に利用できるデータ)」である。
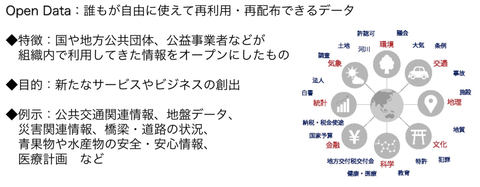
オープンデータとは、誰でも自由に使えて再利用・再配布できるデータだ(図3)。代表例の1つが、国や地方公共団体、公益事業者などが収集し、組織内で利用したり集計値だけを公開したりしていた情報を公開したデータである。公共交通関連情報、地盤データ、災害関連情報、青果物や水産物の安全・安心情報、橋梁や道路の状況、医療計画などもオープンデータになっている。公開の目的は、新たなサービスやビジネスの創出だ。
オープンデータは、ある程度は標準化され、利用するのに分かりやすい表現であることが望ましい。しかし実際にオープンデータを見てみると、加工されたものが多い。競合他社に対してデータ分析で差別化するには、オープンデータになる前のデータを活用しない手はない。筆者はこれを「プレオープンデータ」と呼んでいる。
ここで気をつけなければならないのが、収集時期や公開時期が古いオープンデータだ。その利用は、人間にとってもAIにとっても危険である。古い偏見や差別を持った分析結果が生まれる可能性が高い。あくまでも単なる事実として扱うにとどめるほうが良い。真実かどうかは別問題にある。
政府などが保有し公開したオープンデータなどに対し、最近の経済ニュースなどで頻繁に登場するのが「Alternative Data(オルタナティブ・データ)」である。従来から分析されている財務データではなく、衛星データやクレジットカードの明細データなど、新しい領域のデータであり、公開されていないので価値は高い。大勢が、その価値に気付いておらず、分析対象になる前のデータは、非構造データであることが、ほとんどだ。
データの関係性パターンを知れば分析が容易になる
自らデータを作成したり整理したりする場合は、その表現方法を知らなければならない。逆に、新しいデータを分析する場合は、観測されたデータの関係性パターンを理解すれば分析が容易になる。
前回のベイズ推定の説明でも述べたように、データと数学の関係は深い。数学の基本は「変化を知る」「構造を知る」「空間を知る」である。変化は解析、構造は代数、空間は幾何で解いていく。これら3分野は数学の王道だ。だが、統計の領域が紐解くのは「相関を知る」ことである。
データの関係性パターンを筆者は、上記の数学を活用して「相関」「変化」「構造」「空間」の4つに分けている(図4)。この分け方はデータ分析をするうえでとても役に立つ。今回は、これら4パターンのうち「相関」と「変化」について説明する。