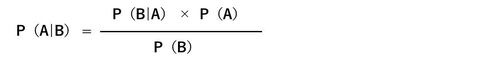未解決な事象の分析に威力を発揮するベイズ推定【第7回】

　第5回で、分類・予測・判別を目的とした決定木分析について説明した。より具体的な顧客像を描き出したときに頻繁に利用する。

　たとえば、市場の調査データなどからも「全種類の缶コーヒーの中で、その商品を選択する確率は25％」と割り出される。これに対し、決定木分析を使って、属性を「頻度」「年齢」「性別」にすれば、「缶コーヒーを毎日飲む40歳代の男性のなかで、その商品を選ぶ人は65％」といった結果が出てくる。あいまいではない、より明確な顧客層が浮かび上がってくる。

　ただし、ここまでは従来の分析手法だ。上記の「25％」「65％」が明確にデータとして取れればよいが、母集団が増え続ける不安定なデータの中では、そこまで“きれいな数字”は存在しない。そこで出てくるのがベイズ推定である。ベイズ推定であれば、不確実な領域に主観的に確率を求め、それを実際に観測されたデータで補完しながら真実に近づいていける。

「ベイズの定理」の数式に惑わされない

　ベイズ推定の基になっている「ベイズの定理」は次の数式で表される。

　この数式をみただけで、難しく感じてしまう方も少なくないだろう。完璧に理解できなくて構わないので、まずはこの数式を簡単に説明だけしておく。

　ある事象Aが起こる確率を「P（A）」と書く。Pは「Probability（確率）」の頭文字だ。適切な解答をいきなり求めるのが難しい場合は、代わりに条件を設定する。この条件をBとすると、条件Bが起こる確率は「P（B）」と書ける。

　このとき、事象Aが起こる中で条件Bが起こる確率を「条件付き確率」と呼び「P（B|A）」と表す。そのときに求めたい確率を「事後確率」と言い「P（A|B）」と書く。これらの関係を表したのが、上の数式になる。

　このベイズの定理を、思考のステップで表すと次のようになる。

Step1：主観的に事前確率P（A）を設定する
Step2：事象Aをあぶり出す条件としてBを創出する
Step3：観測データから条件付き確率P（B|A）を知る
Step4：同様にP（B）を条件ごとに計算する
Step5：ここまでの結果から事後確率P（A|B）を獲得する

　数学的な説明はここまでにして、ベイズの定理を利用する目的である主観的な推論の手順から考えてみよう。主観的な推論の手順は以下である。

手順1：仮説を立てる
手順2：知りたいことをAとする。
手順3：そのままではAが分からないので、代わりに条件Bを設定する
手順4：取得された観測データで補正する

迷惑メールが届く確率をベイズ推定で解いてみる

　例を挙げたほうが分かりやすいので例題も付け加えてみる。

【例題】
A（知りたいこと）：送られてきたメールは迷惑メールかどうか？
B（条件）：メールに「URL」が含まれている

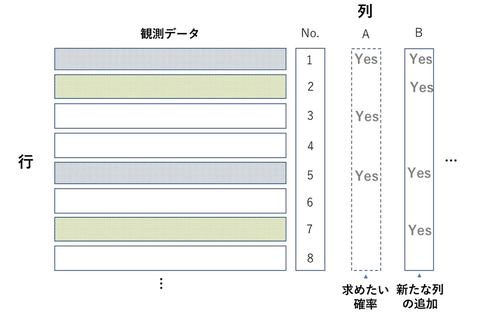
　送られてくるメールに「迷惑メールであるかどうか」の属性が最初から備わっていれば便利だが、そんなことはあり得ない。そこで迷惑メールの条件の1つとして「メールにURLが含まれている」ことを考えた。この「URL付きかどうか」を条件Bとする。これらの求めたい確率と条件とを、実際に取得できた観測データに付け足していく（図１）。

図1：「迷惑メールかどうか」を知るために、観測データに「URL付きかどうか」といった条件を“列”として付与していく