ビッグデータの法則：その3＝数字の魔力【第22回】

　データ分析で競合に差を付けるには、以下の5つの視点が不可欠である。

視点1：違和感に気付く（他との違い、以前との違い、不正の発見など）
視点2：未知のことを探り予測する
視点3：既知のルールを応用する
視点4：適切な仮説を作る
視点5：効率的に分析できるデータ量を知る

　これら５つの視点を磨くために、筆者が使っている法則の中に「数字の魔力」と呼べるものがある。その中から今回は7つを紹介する。

数字の魔力1：ベンフォードの法則

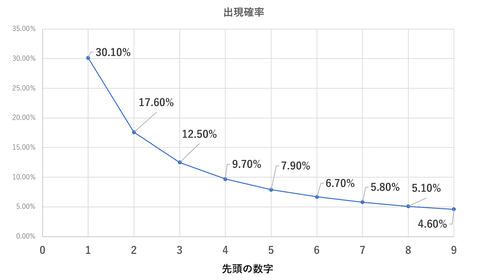
　ランダムに数字を並べ、その先頭に来る数字を調べると、ある奇妙な法則に出会う。普通は「1」から「9」の数字が均等に並びそうなものだが、実際は「1」が一番多い（30.1％）。続いて「2」（17.6％）、「3」（12.5％）、･･･「9」（4.6％）になる（図１）。これが「ベンフォードの法則」で、米国の物理学者ベンフォードが2万ものサンプルを調べて得た。

図1：ランダムに数字を取り出したとき、先頭の数字の出現率を示した「ベンフォードの法則」。不正を見抜いたり未知のことを探るのに有効だ

　ベンフォードの法則は、不正を見抜いたり、未知のことを探ったりする場合にも使える。筆者が国家予算の補助金や委託調査費などのデータを毎日分析した際にも役立った。たとえば予算項目の決算額で、ベンフォードの法則に従わない数字について精査すれば、そこに解が眠っていることが少なくない。

　他にも、数字にまつわるものならば幅広い領域に適用できる。株価、雑誌や新聞に出てくる数字、世界各国の国土面積など、自然現象や社会現象の数値に使える。ただし、電話番号や宝くじの番号のように、あるルールに従って採番された数の並びには当てはまらない。

数字の魔力2：モンモール数

　学校などの席替えをくじ引きで実施した際、誰かが同じ席になる確率は約63％である。同様に、クリスマスに複数人が集まってプレゼントを交換する際に、無作為に行うと誰かが自分が持ってきたプレゼントに当たってしまう確率も約63％になる。これを「モンモール数」という。

　モンモール数は、ある限られた数量を複数の人・部署・組織などで毎回分ける場合、前回との違いを検出する際に、データの中に“違和感”を感じ取るのに役立つ。たとえば、国家予算のデータを分析する際に、年度毎に各予算項目で前年度と同じ決算額になる確率を、このモンモール数で予測しておけば、データのモデリングにおいてデータ入力の間違い発見などに利用できる。

　なお、席替えやプレゼント交換などが成功する確率は約37％であるが、これは、後述する「ネイピア数」の逆数である。

数字の魔力3：黄金比（ 1：（ 1 ＋ √5 ）/ 2 ≒ 1：1.62 ）

　名刺やクレジットカード、文庫本などの縦横比は、概ね「1 : 1.62」である。この比率が一番安定するからで、これを「黄金比」という。

　黄金比は、さまざまなところに登場する。たとえば、直前の2つの数の和を次の数とする数列を考えてみよう。これは「フィボナッチ数列」と呼ぶ（図2）。フィボナッチ数列で、ある程度数が大きくなると、数列の隣り合う数の比が限りなく黄金比に近づいていく。

図2：「フィボナッチ数列」に出現する黄金比。“差”に解が眠っている

　データ分析では通常、数字そのものを重視するが、データ分析で得られた数値の差、あるいは、その差の差を並べることで新たな事実が見つかる。第15回で述べたスパースモデリングでも“差”が重要になる。空間把握や画像分析においては、隣り合うピクセルの色は似ているので、その“差”をとればスパースになるという特性を活用して分析する。

　なお、黄金比の応用で、為替の大きな流れが約162カ月で変わるという説がある。この場合、知られているルール、つまり黄金比を応用することも大切だ。