データに潜む関連性を見いだし将来を予測する【第6回】

　本連載では、データ分析の手順として以下の5つを挙げ、これまでに分類によって当たりをつけ分析対象を絞り込むところまで説明してきた。

手順1：分類によって当たりをつける
手順2：対象を絞り込む
手順3：予測によって影響度を測る
手順4：先を読む
手順5：効果を検証する

　今回は手順3〜5の予測から効果の検証までを取り上げる。特に、数学的な視点による予測と検証の方法をみてみたい。数学は、「必要としない産業はない」と言われるほど応用範囲が広く、様々な産業・業務で活用されている。

手順3：予測して影響度を測る

　データ間の因果関係は、いきなりは分からない。だが相関の強弱は「相関分析」で分かる。一方のデータ（ x ）が増えると、同様に他方のデータ（ y ）も増える関係が"正の相関関係"。逆に、一方のデータが増えると他方のデータが減る関係が"負の相関関係"である。どちらでもない場合を「相関関係がない」という。

　相関関係の強弱は「相関係数」と呼ぶ数字「 -1 ～ +1」で表す。「 -1 」に近いほど負の相関関係になり、「 +1 」に近ければ正の相関関係になる。経験的にいえば、「 -0.2 ～ +0.2 」だと相関関係がないといえる。

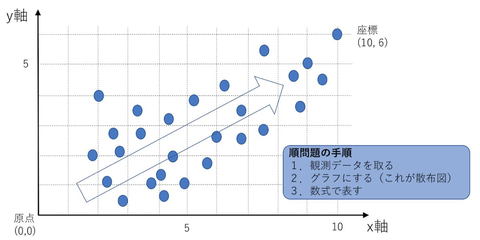
　相関関係を表すデータが散らばったグラフが「散布図」である（図１）。グラフの原点からみた縦と横の距離が「座標」である。この散布図から観測データの関係性をグラフ化し、 y = ax + bやy = cx1 + dx2 + e のような数式に置き換える作業が回帰分析である。数式といっても、原因（ x ）から結果（ y ）を求めるのだから函数である。

図1：「相関分析」で関係の強弱を知る

　回帰分析の流れは以下の通りだ。

（1）観測データを取る
（2）グラフにする
（3）数式y = f（ x ）で表す

　順問題について数学では、グラフの問題を数式（函数）で解く。あるいは、逆問題について、数式（方程式）の問題をグラフで解く。この学問を「解析幾何学」という。著名な数学者であるデカルトとフェルマーが、その創始者とされている。

　数学には３つの"王道"がある。代数、幾何、解析だ。代数は、数字と文字式を、幾何は形と図形を、解析は数式を扱う。解析幾何学は、これら王道の2つを結び付けているところが凄い。そこでのキーワードは座標であり、数式と図形を結び付ける働きをしている。データ分析者は、この基本を最低限押さえなければならない。